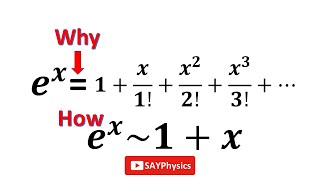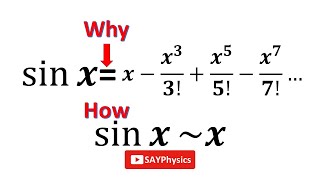Why a function is expanded in series? What is approximation?

The very first thing that we will cover is what is a function? The next question will be why we expand a function?

A function \(f\left( x \right) \) is having an infinite number of components and we expand it into an infinite number of polynomials. We expand this function to know its behavior, with the help of Taylor's series. The behavior of a function can be explained by expending it into its individual components. Any function can be expanded using Taylor's series.

What is a Taylor's series?

If we are having a function \(f\left( x \right) \), it can be expanded as: $$ f\left( x \right) =f\left( a \right) +\frac { f'\left( a \right) }{ 1! } \left( x-a \right) +\frac { f''\left( a \right) }{ 2! } { \left( x-a \right) }^{ 2 }+...+\sum _{ n=0 }^{ \infty }{ \frac { { f }^{ n }\left( a \right) }{ n! } { \left( x-a \right) }^{ n } } $$ For example, $$ f\left( x \right) ={ e }^{ x } $$ It can be expanded by Taylor's series as: $$ { e }^{ x }={ e }^{ 0 }+\frac { { e }^{ 0 } }{ 1! } \left( x-a \right) +\frac { { e }^{ 0 } }{ 2! } { \left( x-a \right) }^{ 2 }+...$$ { e }^{ x }=1+\frac { x }{ 1! } +\frac { { x }^{ 2 } }{ 2! } +\frac { { x }^{ 3 } }{ 3! } +...+\frac { { x }^{ n } }{ n! } $$ Here \(a\) point will be \(0\) because this function is centered at \(x=0\), it starts from that value. Now if we want to understand that how \({ e }^{ x }\) is equal to these infinite number of terms?

If we plot \({ e }^{ x }\) and then we plot 1, as 1 is a constant value, \(x\) is a straight line value and \(x^2\) is parabolic, \(x^3\) is having a different trend then how are they equal?

The third question that we will discuss is what is meant by approximation? We approximate the functions and here the approximation is $$ { e }^{ x }\sim 1+x $$ Higher powers of \(x\) are neglected. In order to see this thing, we can use the plotting software.