Calculate capacitance of a cylindrical capacitor

CAPACITANCE OF CYLINDRICAL CAPACITOR

Consider a cylindrical capacitor of length \(L\). It is constructed with two coaxial cylinders such that inner cylinder has radius \(a\) and charge \(+Q\) while outer cylinder has radius \(b\) and charge \(-Q\) as shown in fig.

The electric field lines come out from positively charged cylinder and enter into negatively charged cylinder.

Now imagine a Gaussian surface in the form of a cylinder of radius r encloses the positively charged inner cylinder of capacitor. The Gaussian cylinde three surfaces.

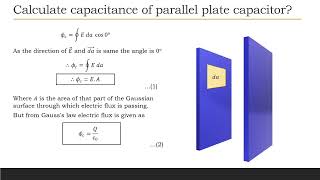
The flux through top-capped Gaussian cylinder having area element \(da\) is $$ \phi_1\ =\oint{\vec{E}.\vec{da}} $$ $$ \ \phi_1\ =\ \int{E\ da\ \cos{90}} $$ $$ \phi_1\ =\ 0 $$ The flux through bottom capped Gaussian cylinder having area element \(da\) is $$ \phi_2\ =\oint{\vec{E}.\vec{da}} $$ $$ \ \phi_2\ =\ \int{E\ da\ \cos{90}} $$ $$ \phi_2\ =\ 0 $$ The flux through curved surface of Gaussian cylinder having area element \(da\) is $$ \phi_3\ =\oint{\vec{E}.\vec{da}} $$ $$ \ \phi_3\ =\ \int{E\ da\ \cos{0}} $$ $$ \phi_3\ =\ E\left(2\pi r\ L\right) $$ Where \(2\pi r\) is circumference of Gaussian cylinder and \(L\) is its length. Net flux through whole Gaussian cylinder is $$ \phi_c\ =\ \phi_1+\phi_2+\phi_3 $$ $$ \phi_c\ =\ 0+0+E\left(2\pi r\ L\right) $$ $$ \phi_c\ =\ E\left(2\pi r\ L\right) $$

. . . . . . . . . . . . . (1)

From Gauss's law $$ \phi_c\ =\ \frac{Q}{\varepsilon_0} $$

. . . . . . . . . . . . . (2)

Comparing eq (1) and eq (2), we get $$ E\left(2\pi r\ L\right)\ =\ \frac{Q}{\varepsilon_0} $$ $$ E\ =\ \frac{Q}{\left(2\pi r\ L\right)\varepsilon_0} $$ The potential related to this electric field of cylindrical capacitor is $$ V\ =\ \int_{a}^{b}{E\ ds} $$ $$ V\ =\ \int_{a}^{b}{\frac{Q}{\left(2\pi r\ L\right)\varepsilon_0}\ dr} $$ $$ V\ =\ \frac{Q}{\left(2\pi\ L\right)\varepsilon_0}\int_{a}^{b}{\frac{1}{r}\ dr} $$ $$ V\ =\ \frac{Q}{\left(2\pi\ L\right)\varepsilon_0}\left[\ln{r}\right]_a^b $$ $$ V\ =\ \frac{Q}{\left(2\pi\ L\right)\varepsilon_0}\left(\ln{b}-\ \ln{a}\right) $$ $$ V\ =\ \frac{Q}{\left(2\pi\ L\right)\varepsilon_0}\ln{\left(\frac{b}{a}\right)} $$ $$ \frac{\left(2\pi\ L\right)\varepsilon_0}{\ln{\left(\frac{b}{a}\right)}}\ =\ \frac{Q}{V} $$ The capacitance of a capacitor is related with voltage as $$ C=\ \frac{Q}{V} $$ Comparing eq(1) and eq(2) $$ C=\ \frac{\left(2\pi\ L\right)\varepsilon_0}{\ln{\left(\frac{b}{a}\right)}} $$ This is the capacitance of a cylindrical capacitor which depends upon length radius "\(a\)" of inner cylinder and radius "\(b\)" of outer cylinder.