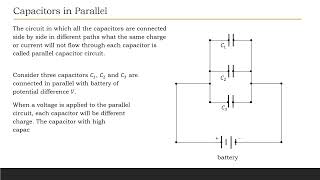
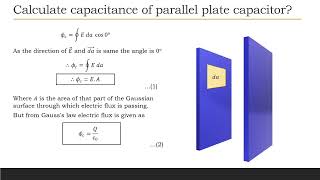
What is relation between Dielectric Constant and Force Between two Charges.

If two charges \({ q }_{ 1 }\) and \({ q }_{ 2 }\) are separated by distance \(r\) in vacuum then electrostatic force between them will be given by the Coulomb law as below:

$${ F }_{ v } = \frac { 1 }{ 4\pi { \epsilon }_{ 0 } } \frac { { q }_{ 1 }{ q }_{ 2 } }{ { r }^{ 2 } } \qquad ...(1)$$ Now if these charges are placed in a medium of absolute permittivity \(\epsilon\) , then electrostatic force between these charges will be $${ F }_{ m } = \frac { 1 }{ 4\pi \epsilon } \frac { { q }_{ 1 }{ q }_{ 2 } }{ { r }^{ 2 } } \qquad ...(2)$$ We know that $$\epsilon = { \epsilon }_{ 0 } { \epsilon }_{ r } =K{ \epsilon }_{ 0 }$$ where \(K\) is dielectric constant or Relative permittivity or specific inductive capacity. or $$K = \frac { \epsilon }{ { \epsilon }_{ 0 } }$$ Now, eqn. (2) becomes, $${ F }_{ m } = \frac { 1 }{ 4\pi K{ \epsilon }_{ 0 } } \frac { { q }_{ 1 }{ q }_{ 2 } }{ { r }^{ 2 } } \qquad ...(3)$$ Dividing eqn. (1) by eqn. (3), $$\frac { { F }_{ v } }{ { F }_{ m } } = \frac { \left( \frac { 1 }{ 4\pi { \epsilon }_{ 0 } } \frac { { q }_{ 1 }{ q }_{ 2 } }{ { r }^{ 2 } } \right) }{ \left( \frac { 1 }{ 4\pi K{ \epsilon }_{ 0 } } \frac { { q }_{ 1 }{ q }_{ 2 } }{ { r }^{ 2 } } \right) } = K$$ Hence, dielectric constant (or relative permittivity) of a medium is defined as the ratio of the electrostatic force between two point charges when placed a certain distance apart in vacuum to the electrostatic force between the same charges when placed same distance apart in a medium.

This means a dielectric reduces the force between two charges.