Calculate capacitance of parallel plate capacitor?

CAPACITANCE OF PARALLEL PLATE CAPACITOR

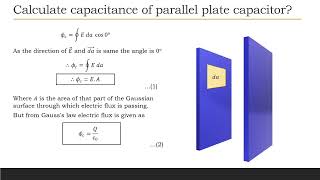
Consider a parallel plate capacitor. The plates are separated by distance \(d\) and each plate has area \(A\). The plate \(a\) has charge \(+Q\) and plate \(b\) has charge \(-Q\). Imagine a Gaussian surface which encloses the charge \(+Q\) of the capacitor plate as shown in fig.

Take small area element \(\vec{da}\) of Gaussian surface. The electric flux through this area element is $$ d\phi_c=\vec{E}.\vec{da} $$ Where \(d\phi_c\) is the electric flux and \(\vec{E}\) is electric field.

To calculate The net flux through Gaussian surface, we need to integrate this equation as $$ \phi_c=\oint{\vec{E}.\vec{da}} $$ As we know the multiple of two vectors is given as $$ \vec{A}.\vec{B}\ =\ A.B\ \cos{\theta} $$ Where \(\theta\) is the angle between the directions of two vectors. Similarly, above equation becomes. $$ \phi_c=E. da. \cos0° $$ As the direction of \(\vec{E}\) and \(\vec{da}\) is same the angle is \(0°\) $$ \therefore\phi_c=\oint{E\ da\ } $$ $$ \therefore\phi_c=E.A $$

. . . . . . . . . . . . . (1)

Where \(A\) is the area of that part of the Gaussian surface through which electric flux is passing. But from Gauss's law electric flux is given as $$ \phi_c=\frac{Q}{\varepsilon_0} $$

. . . . . . . . . . . . . (2)

Where \(Q\) is the charge and \(\varepsilon_0\) is the permittivity of the medium. Comparing equation (1) and (2) we get, $$ E\ A=\frac{Q}{\varepsilon_0} $$ $$ E=\frac{Q}{A\ \varepsilon_0} $$

. . . . . . . . . . . . . (3)

Now lets calculate the potential difference between plates of the capacitor. Potential difference between two points a and b is given by, $$ V_b-V_a=-\int_{a}^{b}{\vec{E}.\vec{ds}} $$ Where \(\vec{E}\) is the electric field and \(\vec{ds}\) is the separation or distance between points \(a\) and \(b\). As previously done lets multiply two vectors again. $$ V_b-V_a=-\int_{a}^{b}{E\ ds\cos{\theta}} $$ The angle between \(ds\) and \(E\) is zero because both have same direction $$ V_b-V_a=-\int_{a}^{b}{E\ ds} $$ For absolute potential between plates, put \(V_b=0\). $$ V=\int_{a}^{b}{E\ ds} $$ The potential between plates having separation \(d\) is $$ V=\int_{0}^{d}{E\ ds} $$ $$ V=E.d $$ Where \(d\) is the total separation between two plates. Lets add the value of \(E\) from equation (3) $$ V=\frac{Q}{A\ \varepsilon_0}d $$ On rearranging the equation $$ \frac{Q}{V}=\frac{A\ \varepsilon_0}{d} $$ \(\frac{Q}{V}\) is the capacitance \(C\) of the parallel plate capacitor. $$ \therefore C=\frac{A\ \varepsilon_0}{d} $$ The capacitance of a parallel plate capacitor depends upon area of plates, separation between plates. In addition, the dielectric medium inserted between plates also affect capacitance of parallel plate capacitor.