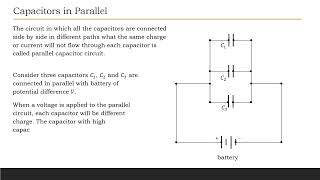
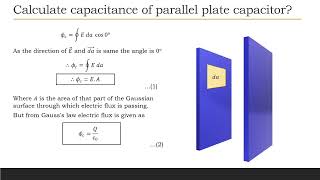
Derive an expression to calculate capacitance of spherical capacitor formed by two concentric shell of radii (a) and (b)?

CAPACITANCE OF SPHERICAL CAPACITOR

Consider a spherical capacitor consists of two spherical concentric shells. The inner spherical shell has radius "\(a\)" and charge \(+Q\). The outer spherical shell has radius "\(b\)" and charge \(-Q\) as shown in fig.

The electric field lines are radial and directed outward from inner shell (+ve plate) to outer shell (-ve plate).

Imagine a Gaussian sphere of radius \(r\) which encloses inner spherical amount of flux diverging out of Gaussian sphere through small area element \(da\) of this Gaussian surface. $$ d\phi_c=\ \vec{E}.\vec{da}\ $$ $$ d\phi_c=\ E.da\ \cos{0}\ $$ $$ d\phi_c=\ E.da\ $$ Net flux through whole Gaussian sphere is $$ \phi_c\ =\oint{E.da} $$ $$ \phi_c=\ E.\left(4\pi r^2\right)\ $$

. . . . . . . . . . . . . (1)

Gauss's law is $$ \phi_c\ =\ \frac{Q}{\varepsilon_0} $$

. . . . . . . . . . . . . (2)

Comparing eq(1) and eq(2) $$ E.\left(4\pi r^2\right)\ =\ \frac{Q}{\varepsilon_0} $$ $$ E\ =\ \frac{Q}{\left(4\pi r^2\right)\varepsilon_0} $$ It is the magnitude of electric field at any point on the Gaussian sphere due to uniform charge distribution of spherical capacitor.

Potential difference between the shells of the capacitor is $$ V\ =\ \int_{a}^{b}{E\ ds} $$ $$ V\ =\ \int_{a}^{b}{\frac{Q}{\left(4\pi r^2\right)\varepsilon_0}\ dr} $$ $$ V\ =\ \frac{Q}{\left(4\pi\right)\varepsilon_0}\int_{a}^{b}{r^{-2}\ dr} $$ $$ V\ =\ \frac{Q}{\left(4\pi\right)\varepsilon_0}\left[\frac{r^{-2+1}}{-2+1}\right]_a^b $$ $$ V\ =\ \frac{Q}{\left(4\pi\right)\varepsilon_0}\left[\frac{r^{-1}}{-1}\right]_a^b $$ $$ V\ =\ \frac{Q}{\left(4\pi\right)\varepsilon_0}\left[\frac{-1}{r}\right]_a^b $$ $$ V\ =\ \frac{Q}{\left(4\pi\right)\varepsilon_0}\left[\frac{1}{a}-\frac{1}{b}\right] $$ $$ V\ =\ \frac{Q}{\left(4\pi\right)\varepsilon_0}\left[\frac{b-a}{ab}\right] $$ $$ \frac{Q}{V}=\ \left(4\pi\right)\varepsilon_0\left[\frac{ab}{b-a}\right] $$

. . . . . . . . . . . . . (3)

The capacitance of spherical capacitor is $$ \frac{Q}{V}=C $$

. . . . . . . . . . . . . (4)

Comparing eq (3) and eq (4) $$ C=\ \left(4\pi\right)\varepsilon_0\left[\frac{ab}{b-a}\right] $$ This is capacitance of spherical capacitor. It depends upon radius of inner shell and radius of outer spherical shell of capacitor.

ISOLATED SPHERE:

The positively charged inner spherical shell is called isolated sphere negatively charged outer spherical shell is moved at infinity distance. The potential is $$ V\ =\ \frac{Q}{\left(4\pi\right)\varepsilon_0}\left[\frac{1}{a}-\frac{1}{b}\right] $$ $$ V\ =\ \frac{Q}{\left(4\pi\right)\varepsilon_0}\left[\frac{1}{a}-\frac{1}{\infty}\right] $$ $$ V\ =\ \frac{Q}{\left(4\pi\right)\varepsilon_0a} $$ $$ \frac{Q}{V}=\ \left(4\pi\right)\varepsilon_0a $$ $$ C=\ \left(4\pi\right)\varepsilon_0a $$ This is capacitance of isolated sphere.